时间复杂度 可以理解为进行了多少次常数操作的指标(加、减、乘、除、数组寻址),只会取通项公式系数最高
常数操作为 O(1)
冒泡排序为类似于等差数列,等差数列通项公式 Sₙ=na₁+n(n-1)d/2 即为 O(n^2)
二分查找为 O(logN)
异或 1、异或满足结合律 与分配律
2、相同数字异或为0,任何数异或0 都为任何数
3、可以理解为无进位相加
代码值的相互替换可以不生成新的变量 (内存地址不可以相同,如果相同则为自己异或自己 结果为0 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 let a = 10 ;let b = 9 ;a = a ^ b; b = a ^ b; a = a ^ b;
题目:有一个数组 有N个数出现偶数次、1个数出现奇数次
1 2 3 4 5 6 7 8 9 10 let arr = [1 ,2 ,3 ,3 ,4 ,2 ,1 ,1 ,1 ,3 ,4 ];let eor = 0 ;arr.forEath (item => eor ^= item; }) console .log ("出现奇数次的数" ,eor)
题目:有一个数组 有N个数出现偶数次、2个数出现奇数次
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 let arr = [1 ,2 ,3 ,3 ,4 ,2 ,1 ,1 ,1 ,3 ,4 ,5 ];let eor = 0 ;arr.forEath (item => eor = eor ^ item; }) let rightOne = eor & (~eor + 1 );let onlyOne = 0 ;arr.forEath (item => if (item & rightOne === 0 ){ onlyOne ^= item; } }) let b = eor ^ onlyOne;
排序 选择排序 第一步,0 到n-1 获取最小值
第二步,将最小值索引与索引0交换
第三步,1到n - 1 获取最小值
第四步,重复步骤二 交换索引为1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 const arr = [1 ,7 ,5 ,2 ,0 ,3 ,6 ,4 ]let index = 0 ;const selectSort = (arr:number [],index:number ) => { if (arr === null || arr.length < 2 ) return arr; let minIndex = index; for (let i = index; i < arr.length ; i++){ if (arr[i] < arr[minIndex]){ minIndex = i; } } let temp = arr[index]; arr[index] = arr[minIndex]; arr[minIndex] = temp; if (index + 1 < arr.length ){ return selectSort (arr,index += 1 ) }else { return arr; } } console .log (selectSort (arr,index));const selectSort1 = ( for (let i = 0 ; i < arr.length ; i++){ let minIndex = i; for (let j = i + 1 ;j < arr.length ; j++){ minIndex = arr[minIndex] > arr[j] ? j : minIndex; } let temp = arr[i]; arr[i] = arr[minIndex]; arr[minIndex] = temp; } }
冒泡排序 第一步:将0与arr.length位置进行比较判断,如果n小于n+1,就进行交换,第一轮交换结束后,数组的最后一位为最大值
第二步:将0与arr.length - 2重复步骤一
插入排序 第一步、判断0,1位置是否有序,1位置小于0位置 ,则互换
第二步、判断0,2位置是否有序,无序则比对1位置小则交换,大则结束;比较0位置小则交换,大则结束;索引小于0则结束
第n步、判断0,n位置是否有序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 const arr = [1 ,7 ,5 ,2 ,0 ,3 ,6 ,4 ]const insertSort = ( for (let i = 1 ; i < arr.length ; i++){ let index = i; while (index - 1 >= 0 && arr[index - 1 ] > arr[index]){ let temp = arr[index]; arr[index] = arr[index -1 ]; arr[index - 1 ] = temp; index --; } } } insertSort ();console .log (arr);
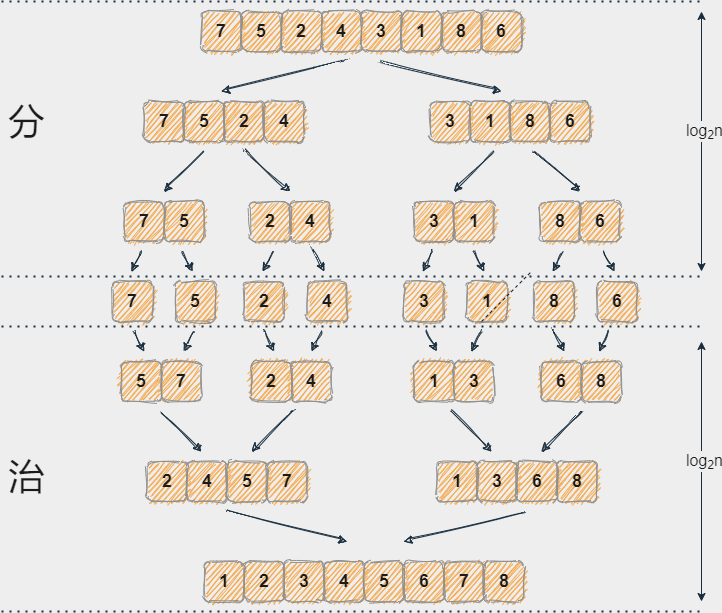
归并排序
第一步、将数组根据中间索引进行拆分,将拆分后的左右两数组继续进行拆分直至数组长度为1
第二步、合并两个数组 按两个被拆分的数组进行处理,定义L指针、R指针 分别执行左右两个数组,将数据保存到temp临时数组中,做一下两个数组的越界处理,将temp数组中的内容替换到arr数组中
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 function merge (arr: number [],left: number ,right: number ,middle: number ,temp: number [] ) { let index = 0 ; let R = middle + 1 ; let L = left; while (L <= middle && R <= right) { temp[index++] = arr[L] < arr[R] ? arr[L++] : arr[R++]; } while (L <= middle) { temp[index++] = arr[L++]; } while (R <= right) { temp[index++] = arr[R++]; } for (index = 0 ; left + index <= right; index++) { arr[left + index] = temp[index]; } } function mergeSort (arr: number [] ) { const temp : number [] = []; const process = (arr: number [],left: number ,right: number ,temp: number [] ) => { if (left >= right) return ; let middle = parseInt (`${(left + right) / 2 } ` ); process (arr, left, middle, temp); process (arr, middle + 1 , right, temp); merge (arr, left, right, middle, temp); }; process (arr, 0 , arr.length - 1 , temp); } const arr = [1 , 5 , 2 , 6 , 8 , 4 , 7 , 9 , 3 , 99 , -1 ];mergeSort (arr);console .log (arr);
快速排序 第一步、找一个基准值
第二步、从剩余数组中区分出大于基准值与小于基准值的数组
第三步、拼接 递归大于小于基准值的数组与原基准值
1 2 3 4 5 6 7 8 9 10 function quickSort (arr:number [] ):number []{ if (arr.length < 2 ) return arr; const flag = arr[0 ]; let maxArr = arr.slice (1 ).filter (item => let minArr = arr.slice (1 ).filter (item => return quickSort (minArr).concat ([flag]).concat (quickSort (maxArr)); } const arr = [1 , 5 , 2 , 6 , 8 , 4 , 7 , 9 , 3 , 99 , -1 ]; console .log (quickSort (arr));
前置问题 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 const arr = [1 , 5 , 2 , 6 , 8 , 4 , 7 , 9 , 3 , 99 ]; const num = 5 ; function generatorArr (arr,num) { let L = -1 ; for (let i = 0 ; i < arr.length ; i++){ if (arr[i] <= num){ let temp = arr[i]; arr[i] = arr[L + 1 ]; arr[L + 1 ] = temp; L++; } } } generatorArr (arr,num)console .log (arr);const arr1 = [1 , 5 , 2 , 6 , 8 , 4 , 7 , 9 , 3 , 99 , 5 ]; const num1 = 5 ; function netherlandsFlag (arr:number [],num:number ){ let index = 0 ; let L = -1 ; let R = arr.length ; while (arr[index] !== arr[R]){ if (arr[index] < num){ let temp = arr[index]; arr[index] = arr[L + 1 ]; arr[L + 1 ] = temp; index++; L++; }else if (arr[index] === num){ index++; }else { let temp = arr[index]; arr[index] = arr[R - 1 ]; arr[R - 1 ] = temp; R--; } } } netherlandsFlag (arr1,num1)console .log (arr1);
通过问题1可推出快速排序1版本,设置数组中最后一个值为指定值,将剩余数组进行左右划分,再将右侧数组的第一个与指定值互换,递归左右数组
通过问题2可推出快速排序2版本,设置数组中最后一个值为指定值,利用荷兰国旗问题,找到右侧数组的第一个与指定值互换,然后再递归左右数组,中心数组不变(指定值的集合)
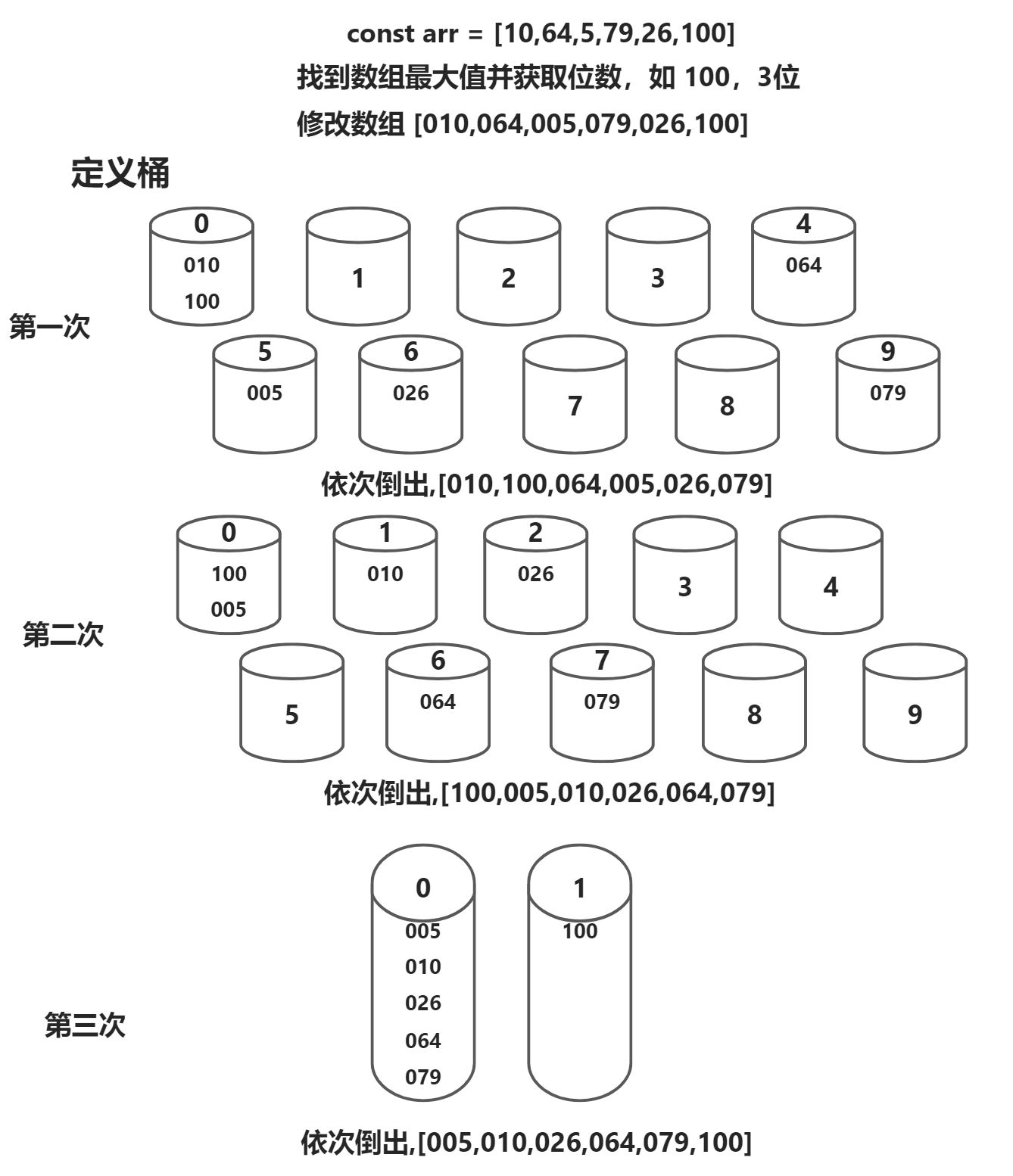
堆排序 桶排序 题目1:数组X中每一位的值都在【0,100】区间内,进行排序
解题思路:计数排序
步骤一、生成一个长度为101,每一位都是0的数组Y,遍历X数组根据X数组的值,使Y数组对应索引加一
步骤二、根据Y索引的对应的值 如 index 存在 Y[index]个值
解题思路:奇数排序
步骤一、找到最大值的位数,将小于该位数的值,前面补0直至满足最值大位数如最大值100,其他数075
步骤二、生成桶,并将数组每一位个位数放到对应尾数值得桶中
步骤三、根据桶的索引依次将数组倒出、再根据每一位值得十位数放到桶中
步骤四、根据桶的索引依次将数组倒出、再根据每一位值得百位数放到桶中
………
直至将最大值得第一位放入桶中再从左到右再倒出
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 function getDigit (num: number ): number { let index = 0 ; while (num > 1 ) { num /= 10 ; index++; } return index; } function bucketSort (arr: number [] ) { let index = 0 ; const digit = getDigit (Math .max (...arr)); const temp : number [] = []; while (index <= digit) { let bucket : number [][] = [[], [], [], [], [], [], [], [], [], []]; let tempIndex = 0 ; for (let i = 0 ; i < arr.length ; i++) { const bucketIndex = arr[i].toString ()[arr[i].toString ().length - index - 1 ] ?? 0 ; bucket[bucketIndex].push (arr[i]); } for (let i = 0 ; i < bucket.length ; i++) { if (bucket[i].length > 0 ) { bucket[i].forEach ((item ) => { temp[tempIndex++] = item; }); } } arr = temp; index++; } return temp; } const arr = [10 , 5 , 7 , 24 , 16 , 50 , 13 , 46 , 100 ];console .log (bucketSort (arr));
查找 二分查找 从有序数组 中找到对应的数值,或者是无序 但是可以肯定某一侧肯定存在查找的值,就可以二分
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 function binarySearch (arr,num) { let start = 0 ; let end = arr.length - 1 ; let middle = parseInt ((arr.length - 1 ) / 2 ); while (start < end){ middle = parseInt ((end + start) / 2 ) if (arr[middle] < num){ start = middle + 1 ; }else if (arr[middle] > num){ end = middle - 1 ; }else { return true ; } } if (start === end) { return arr[start] == num ? true : false ; } } const arr = [1 ,2 ,3 ,3 ,4 ,5 ,6 ,7 ,9 ];const num = 0 console .log (binarySearch (arr,num))
递归查找 master公式求解递归时间复杂度 (子问题规模一致)
N 表示数据量
a 表示调用函数次数
T(N/b) 表示子问题规模
d 表示其他代码时间复杂度
数据结构 1、数组:便于寻址,不便于增删数据
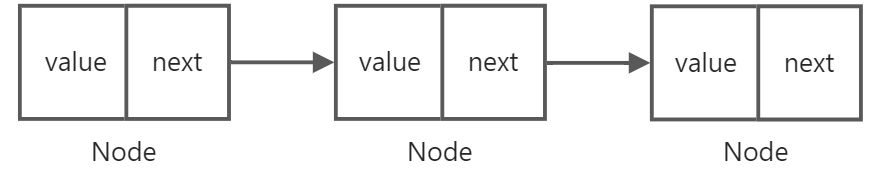
2、链表:便于增删数据,不便于寻址
链表结构
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 const next = (head ) => { if (head === null || head.next === null ) return head; let newHead = next (head.next ); head.next .next = head; head.next = null ; return newHead } this .head = next (this .head )return this .head ;if (this .head &&this .head .next ){ let head = this .head ; let newHead = null ; while (head!= null ){ let tem = head.next ; head.next = newHead; newHead = head; head = tem; } this .head = newHead return newHead; }else { return this .head ; }
堆结构 在逻辑概念上 可以理解为是一个完全二叉树( 树的层级都是满的,如果不满也是从左往右依次变满 )
堆结构就是用数组实现的完全二叉树结构
完全二叉树中如果每颗子树的最大值都在顶部就是大跟堆
完全二叉树中如果每颗子树的最小值都在顶部就是小跟堆
堆结构具有insert操作、heapify堆化操作
优先级队列结构就是堆结构
因此 节点的左节点满足 2 * i + 1、右节点满足2 * i + 2、父节点满足 ( i - 1 )/ 2
大根堆 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 class Heap { private size = 0 ; private heapList = []; constructor (list?:[] ){ if (list){ for (let i in list){ this .add (i); } } } private compareParent (index ){ while (this .heapList [index] > this .heapList [(index - 1 ) / 2 ]){ let temp = this .heapList [index]; this .heapList [index] = this .heapList [(index - 1 ) / 2 ] this .heapList [(index - 1 ) / 2 ] = temp; index = (index - 1 ) / 2 ; } } add (num ) { this .heapList .push (num); if (this .heapList .length > 1 ){ this .compareParent (this .size ) } this .size += 1 ; } getSize ( return this .size ; } getAllNode ( return [...this .heapList ]; } peek ( return this .heapList [0 ]; } pop ( let retValue = this .peek (); this .size -= 1 ; this .heapList [0 ] = this .heapList [this .heapList .length - 1 ]; this .heapList .pop (); this .heapify (0 ); return retValue; } heapify (index ){ let left = index * 2 + 1 ; while (left < this .size ){ let largest = left + 1 < this .size && this .heapList [left] < this .heapList [left + 1 ] ? left + 1 : left; largest = this .heapList [index] < this .heapList [largest] ? largest : index; if (index === largest){ break ; } let temp = this .heapList [index]; this .heapList [index] = this .heapList [largest] this .heapList [largest] = temp; index = largest; left = index * 2 / 1 ; } } sort ( if (this .heapList .length < 2 ) return this .heapList ; let temp = this .heapList [0 ]; this .heapList [0 ] = this .heapList [this .size - 1 ]; this .heapList [this .size - 1 ] = temp; this .size -= 1 ; while (this .size > 0 ){ this .heapify (0 ); let temp = this .heapList [0 ]; this .heapList [0 ] = this .heapList [this .size - 1 ]; this .heapList [this .size - 1 ] = temp; this .size -= 1 ; } } }
随机数 Math.random 会等概率生成 [0,1) 之间的一个小数
Math.random() * N 会等概率生成 [0,N)之间的一个小数
parseInt(Math.random() * N) 会等概率生成 [0,N - 1]之间的一个整数
等概率发生器 我们可以通过等概率发生器将1-5 随机生成的函数 转为 0 - 1 等概率随机生成函数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 const f1 = parseInt ((Math .random () * 5 )) +1 const f2 = ( let c = 0 ; do { c = f1 () }while (c === 3 ) return c > 3 ? 1 : 0 ; } const f3 = ( let c = 0 ; do { c = f2 (); }while (c === 0 ) return c; }
将01不等概率转为等概率 假设 fn为不等概率的产生0,1 , 将fn执行两次 1、0 返回 1;0、1返回0;去除0、0与1、1
1 2 3 4 5 6 7 8 9 10 const f =Math .random () < 0.77 ? 0 : 1 ;const f1 = ( let c = 0 ; do { c = f () }while (c === fn ()) return c; }
对数器 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 function generatorArr (maxSize: number , maxValue: number ) { const arr = []; const length = parseInt (`${Math .random() * (maxSize + 1 )} ` ); for (let i = 0 ; i < length; i++) { arr.push (parseInt (`${Math .random() * (maxValue + 1 )} ` )); } return arr; } function copyArr (arr: number [] ) { if (arr && arr.length === 0 ) return arr; let newArr = []; for (let i = 0 ; i < arr.length ; i++) { newArr[i] = arr[i]; } return newArr; } function defaultValidtor (arr: number [] ) { return arr.sort ((a, b ) => a - b); } interface LogarithmProps { maxSize?: number ; maxValue?: number ; validtorSort : (arr: number [] ) => void ; debug?: boolean ; } function logarithm (options: LogarithmProps ) { const debug = options.debug ? options.debug : false ; const testCount = debug ? 10 : 500000 ; const maxSize = debug ? 10 : options.maxSize ?? 100 ; const maxValue = debug ? 10 : options.maxValue ?? 100 ; let complete = true ; for (let i = 0 ; i < testCount; i++) { let arr1 = generatorArr (maxSize, maxValue); let arr2 = copyArr (arr1); debug && console .log (`arr1 : ${arr1} \n arr2 : ${arr2} ` ); options.validtorSort (arr1); defaultValidtor (arr2); debug && console .log (`排序后 arr1 : ${arr1} \n 排序后 arr2 : ${arr2} ` ); let i = 0 ; while (i < arr1.length && complete) { if (arr1[i] !== arr2[i]) { complete = false ; } i++; } if (!complete) break ; } return complete; } const insertSort = (arr: number [] ) => { for (let i = 1 ; i < arr.length ; i++) { let index = i; while (index - 1 >= 0 && arr[index - 1 ] > arr[index]) { let temp = arr[index]; arr[index] = arr[index - 1 ]; arr[index - 1 ] = temp; index--; } } }; logarithm ({ validtorSort : insertSort, debug : true , });
前缀数组 假设有一个数组arr,用户总是频繁查询数组中某一段的累加和,如何设计数据结构更加方便
let arr = [2,1,7,5,8,6,4,3]
前缀和数组
1 2 3 4 5 6 7 8 9 10 11 const preSumArr = [];const RangeSum = (arr:number [] ) => { for (let i = 0 ; i < arr.length ; i++){ preSumArr[i] = preSumArr[i-1 ] + arr[i] } } const preSum = (L:number ,R:number ) => { return L === 0 ? preSumArr[R] : preSumArr[R] - preSumArr[L] }
算法技巧 单链表结构常用处理
1、判断一个链表是否为回文结构 题目:给定一个单链表的头节点head,请判断是否为回文结构
例子:1->2->1 返回true,1->2->2->1 返回true,1->2->3 返回false
快慢指针:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 class Node { public value :number ; public next :Node |null ; constructor (value:number ,next:Node|null ){ this .value = value; this .next = next; } } function isPalindrome1 (head:Node ){ const stack :Node [] = []; let cur = head; while (cur !== null ){ stack.push (cur); cur = cur.next ; } while (head !== null ){ if (head.value !== stack.pop ().value ){ return false ; } head = head.next ; } return true ; } function isPalindrome2 (head:Node ){ if (head == null || head.next == null ) return true ; let right = head.next ; let cur = head; while (cur.next !==null && cur.next .next !== null ){ right = right.next ; cur = cur.next .next ; } const stack :Node [] = []; while (right !== null ){ stack.push (rigth); rigth = right.next ; } while (stack.length > 0 ){ if (head.value !== stack.pop ().value ){ return false ; } head = head.next ; } return true ; } function isPalindrome3 (head:Node ){ if (head == null || head.next == null ) return true ; let n1 = head; let n2 = head; while (n2.next !== null && n2.next .next !== null ){ n1 = n1.next ; n2 = n2.next .next ; } n2 = n1.next ; n1.next = null ; let n3 = null ; while (n2 != null ){ n3 = n2.next ; n2.next = n1; n1 = n2; n2 = n3; } n3 = n1; n2 = head; let result = true ; while (n1 !== null && n2 !== null && result){ if (n1.value != n2.value ){ result = false ; } n1 = n1.next ; n2 = n2.next ; } n1 = n3.next ; n3.next = null ; while (n1 !== null ){ n2 = n1.next ; n1.next = n3; n3 = n1; n1 = n2; } return res; }
2、将单向链表按某值划分为左侧小于、中间等于、右侧大于结构 题目:给定一个单链表的头节点head,节点的值类型是整数,再给定一个整数pivot。实现一个调整链表的函数,将链表调整为左部门都是值小于pivot的节点,中间部门都是值等于pivot的节点,右部门都是值大于pivot的节点
【进阶】:在实现原问题功能的基础上增加如下的要求
【要求】:调整后所有小于、大于、等于pivot的节点之间的相对顺序和调整前一样
【要求】:时间复杂度O(N),额外空间复杂度O(1)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 class Node { public value :number ; public next :Node |null ; public rand :Node |null ; constructor (value:number ,next:Node|null ,rand:Node|null ){ this .value = value; this .next = next; this .rand = rand; } } function listPartition (head:Node,pivot:number ){ let startH :Node |null = null ; let startE :Node |null = null ; let middleH :Node |null = null ; let middleE :Node |null = null ; let endH :Node |null = null ; let endE :Node |null = null ; let next :Node |null = null ; while (head !== null ){ next = head.next ; head.next = null ; if (head.value < pivot){ if (startH === null ){ startH = head; startE = head; }else { startE.next = head; startE = head; } }else if (head.value === pivot){ if (middleH === null ){ middleH = head; middleE = head; }else { middleE.next = head; middleE = head; } }else { if (endH === null ){ endH = head; endE = head; }else { endE.next = head; endE = head; } } head = next; } if (startE !== null ){ startE.next = middleH; middleE = middleE === null ? startE : middleE; } if (middleE !== null ){ middleE.next = endH; } return startH !== null ? startH : (middleH !== null ? middleH : endH) }
3、复制含有随机指针节点的链表 题目:一种特殊的单链表节点类描述如下
1 class Node { next :Node ,rand :Node ,value :number }
rand指针是单链表节点结构中新增的指针,rand可能指向链表中的任意一个节点,也可能指向null。给定一个由Node节点类型组成的无环单链表的头节点head,请实现一个函数完成这个链表的复制,并返回复制的新链表的头节点。
【要求】:时间复杂度O(N),空间复杂度O(1)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 class Node { public value :number ; public next :Node |null ; constructor (value:number ,next:Node|null ){ this .value = value; this .next = next; } } function copyListWithRand (head:Node ){ let map = new Map <Node ,Node >(); let cur = head; while (cur !== null ){ map.set (cur,new Node (cur.value ,null )); cur = cur.next ; } cur = head; while (cur !== null ){ map.get (cur).next = map.get (cur.next ); map.get (cur).rand = map.get (cur.rand ); cur = cur.next ; } return map.get (head); } function copyListWithRand2 (head:Node ){ if (head === null ) return null ; let cur = head; let next :Node |null = null ; while (cur !== null ){ next= cur.next ; cur.next = new Node (cur.value ,next); cur = next; } cur = head; let curCopy = null ; while (cur !== null ){ next = cur.next .next ; curCopy = cur.next ; curCopy.rand = cur.rand != null ? cur.rand .next : null ; cur = next; } let result = head.next ; cur = head; while (cur !== null ){ next = cur.next .next ; curCopy = cur.next ; cur.next = next; curCopy.next = next !== null ? next.next : null ; cur = next; } return res; }
4、两个单链表相交的一系列问题 题目:给定两个可能有环也可能无环的单链表,头节点head1和head2。请实现一个函数,如果两个链表相交,请返回相交的第一个节点。如果不相交返回null
【要求】:如果两个链表长度之和为N,时间复杂度O(N),空间复杂度O(1)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 function getLoopNode (head:Node ){ if (head === null || head.next === null ) return null ; let n1 = head.next ; let n2 = head.next .next ; while (n1 !== n2){ if (n2.next === null || n2.next .next === null ) return null ; n2 = n2.next .next ; n1 = n1.next ; } n2 = head; while (n1 != n2){ n1 = n1.next ; n2 = n2.next ; } return n1; } function noLoop (head1:Node,head2:Node ){ if (head1 === null || head2 === null ) return null ; let cur1 = head1; let cur2 = head2; let n = 0 ; while (cur1.next !== null ){ n++; cur1 = cur1.next ; } while (cur2.next !== null ){ n--; cur2 = cur2.next ; } if (cur1 != cur2) return null ; cur1 = n > 0 ? head1 : head2; cur2 = cur1 === head1 ? head2 :head; n = Math .abs (n); while (n !== 0 ){ n--; cur1 = cur1.next ; } while (cur1 !== cur2){ cur1 = cur1.next ; cur2 = cur2.next ; } return cur1; } function bothLoop (head1:Node,head2:Node,loop1:Node,loop2:Node ){ let cur1 :Node |null = null ; let cur2 :Node |null = null ; if (loop1 === loop2){ cur1 = head1; cur2 = head2; let n = 0 ; while (cur1 != loop1){ n++; cur1 = cur1.next ; } while (cur2 != loop2){ n--; cur2 = cur2.next ; } cur1 = n > 0 ? head1 : head2; cur2 = cur1 === head1 ? head2 :head; n = Math .abs (n); while (n !== 0 ){ n--; cur1 = cur1.next ; } while (cur1 !== cur2){ cur1 = cur1.next ; cur2 = cur2.next ; } return cur1; }else { cur1 = loop1.next ; while (cur1 !== loop1){ if (cur1 == loop2){ return loop1 } cur1 = cur1.next ; } return null ; } } function getIntersetcNode (head1:Node,head2:Node ){ if (head1 === null || head2 === null ) return null ; let loop1 = getLoopNode (head1); let loop2 = getLoopNode (head2); if (loop1 === null && loop2 === null ){ return noLoop (head1,head2); } if (loop1 !== null && loop2 !== null ){ return bothLoop (head1,head2,loop1,loop2); } return null ; }
二叉树 1 class Node <T > { value:T,left:Node |null ,right:Node |null }
用递归与非递归方式实现二叉树的先序、中序、后序遍历 如何直观的打印二叉树 如何完成宽度有限的二叉树遍历
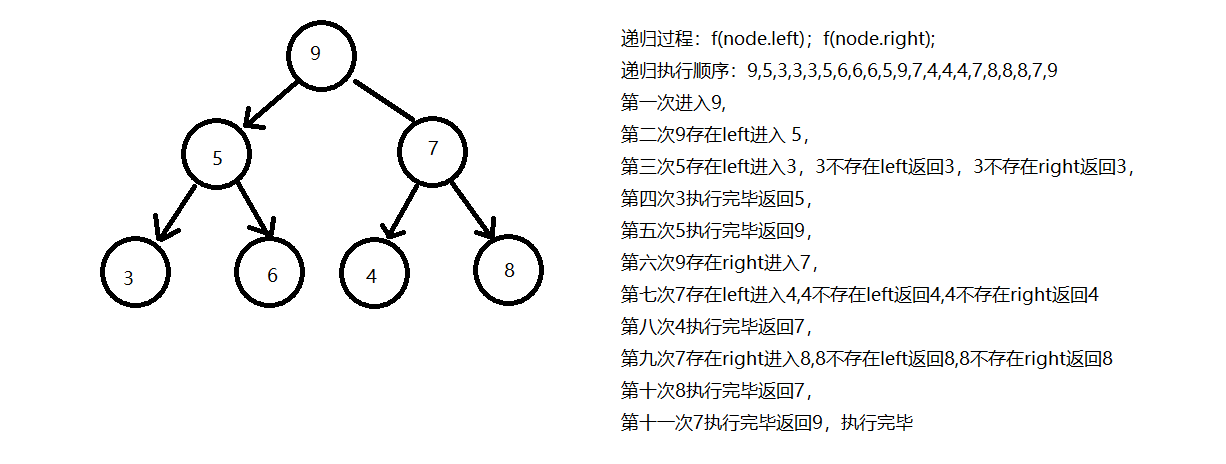
先序遍历 先进入头节点,再进入左子树,返回头节点进入右子树
头 -> 左 -> 右
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 function preorder (head:Node ){ if (head === null ){ return null ; } console .log (head); preorder (head.left ); preorder (head.right ); } function preorder (head:Node|null ){ if (head === null ) return null ; const stack :Node [] = [head]; while (stack.lenght > 0 ){ let cur = stack.pop (); console .log ("处理Node :" ,cur.value ); cur.right && stack.push (cur.right ); cur.left && stack.push (cur.left ); } }
中序遍历 先进入左子树,然后头节点,然后再进入右子树
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 function middleOrder (head:Node ){ if (head === null ){ return null ; } preorder (head.left ); console .log (head); preorder (head.right ); } function middleOrder (head:Node ){ if (head !== null ){ const stack :Node [] = [head]; while (stack.lenght > 0 || head !== null ){ if (head !== null ){ stack.push (head); head = head.left ; }else { head = stack.pop (); console .log (head.value ); head = head.right ; } } } }
后序遍历 先进入左子树,然后右子树,然后打印头节点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 function postOrder (head:Node ){ if (head === null ){ return null ; } preorder (head.left ); preorder (head.right ); console .log (head); } function postOrder (head:Node|null ){ if (head === null ) return null ; const stack :Node [] = [head]; const auxiliary :Node [] = []; while (stack.lenght > 0 ){ let cur = stack.pop (); auxiliary.push (cur); cur.left && stack.push (cur.left ); cur.right && stack.push (cur.right ); } while (auxiliary.lenght > 0 ){ let cur = auxiliary.pop (); console .log ("处理cur :" ,cur.value ) } }
宽度优先遍历 使用队列(先进先出)先放head 弹出head,然后先放左再放右
1 2 3 4 5 6 7 8 9 function widthFirstOrder (head:Node ){ const queue :Node [] = [head]; while (queue.lenght > 0 ){ let cur = queue.shift (); console .log ("需要处理的value :" ,cur.value ) cur.right && queue.unshift (cur.right ); cur.left && queue.unshift (cur.left ); } }
获取二叉树的最大宽度节点个数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 function getMaxWidthNodeSize (head:Node ) { if (head === null ) return ; const queue :Node [] = [head]; const levelMap = new Map <Node ,number >(); levelMap.set (head,1 ); let curLevel = 1 ; let curLevelNodes = 0 ; let max = -1 ; while (queue.lenght > 0 ){ let cur = queue.shift (); let curNodeLevel = levelMap.get (cur); if (curNodeLevel === curLevel){ curLevelNodes++; }else { max = Math .max (max,curLevelNodes); curLevel++; curLevelNodes = 0 ; } if (cur.left ){ levelMap.set (cur.left ,curNodeLevel + 1 ); queue.unshift (cur.left ); } if (cur.right ){ levelMap.set (cur.right ,curNodeLevel + 1 ); queue.unshift (cur.right ); } } }
搜索二叉树 满足一棵树左子树都比当前Node小,右子树都比当前Node大
问题:如何判断一棵树是搜索二叉树
使用中序遍历,左 -> 中 -> 右 可以只知道是都是升序的
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 let preValue = Number .MIN_VALUE ; function isBST (head:Node ){ if (head === null ) return true ; let isLeftBst = isBST (head.left ); if (!isLeftBst) return false ; if (head.value < preValue) { return false }else { preValue = head.value } return isBst (head.right ); } function isBST1 (head:Node ){ const temp :Node [] = [] const process = (head:Node ) => { if (head === null ) return ; precess (head.left ); temp.push (head); precess (head.right ); } process (head); for (let i = 1 ; i < temp.length ; i++){ if (temp[i].value < temp[i - 1 ].value ){ return false } } return true ; } function isSearchBinaryTree (head:Node ) { return process (head :Node ).isBST ; } function process (head:Node ){ if (head === null ){ return null ; } let leftInfo = process (head.left ); let rightInfo = process (head.right ); let max = Number .MIN_VALUE ; let min = Number .MIN_VALUE ; if (leftInfo !== null ){ max = Math .max (head.value ,leftInfo.max ); min = Math .min (head.value ,leftInfo.min ); } if (rightInfo !== null ){ max = Math .max (head.value ,rightInfo.max ); min = Math .min (head.value ,rightInfo.min ); } let isBST = (leftInfo !== null ? (leftInfo.isBST || head.value > leftInfo.max ) : true ) && (rightInfo!== null ? (rightInfo.isBST || head.value < rightInfo.min ) : true ); return {max,min,isBST} }
完全二叉树 二叉树从左到右存在节点,或者是个满二叉树
问题:如何判断二叉树是否是满的
二叉树按宽度遍历,
如果存在有右子树没有左子树 则返回false
如果不满足上述问题时,且左右节点不全的情况下,接下来遇到的所有节点都必须是叶子节点(度为0的节点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 function CompleteBinaryTree (head:Node ){ if (head === null ) return true ; const queue :Node [] = [head]; let leaf = false ; let l :Node |null = null ; let r :Node |null = null ; while (queue.length > 0 ){ head = queue.shift (); l = head.left ; r = head.right ; if ((leaf && (l!==null ||r!==null ))||(l!==null ||r!==null )){ return false ; } if (l !== null ) queue.unshift (l); if (r !== null ) queue.unshift (r); if (l == null || r== null ){ leaf = true ; } } return true ; }
满二叉树 满二叉树满足 L为深度,N为节点个数 满足
问题:求满二叉树
可以先求出L深度,N二叉树的节点个数,然后判断是否满足
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 function fullBinaryTree (head:Node ){ const {deep,count} = process (head :Node ); let targetCount = 2 ** deep - 1 ; return targetCount === count; } function process (head:Node ){ if (head === null ){ return {deep :0 ,count :0 }; } let leftInfo = process (head.left ); let rightInfo = process (head.right ); let deep = Math .max (leftInfo.deep ,rightInfo.deep ) + 1 ; let count = leftInfo.deep + rightInfo.deep + 1 ; return {deep,count}; }
平衡二叉树 满足左子树的高度与右子树的高度差都不超过1
问题:判断是否为平衡二叉树
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 function isBalanceTree (head:Node ){ return process (head).isbanlance ; } function process (head:Node ){ if (head === 0 ){ return {height :0 ,isbanlance :true } } let leftInfo = process (head.left ); let rightInfo = process (head.right ); let height = Math .max (leftInfo.height ,rightInfo.height ) + 1 ; let isbanlance = leftInfo.isbanlance && rightInfo.isbanlance && Math .abs (leftInfo.height - rightInfo.height ) <= 1 return {height,isbanlance} }
解决树形DP问题 使用递归方式,找到需要使用的共用属性递归返回,类似于事件冒泡,从叶子结点开始往上收集,收集到根时进行处理
找到O1、O2节点的公共祖先 问题1、O1是O2的祖先或者O2是O1的祖先
问题2、O1与O2存在共同祖先
1 2 3 4 5 6 7 8 9 10 11 function getCommonAncestor (head:Node,O1:Node,O2:Node ){ if (head === null || head === O1 || head === O2 ){ return head; } let leftInfo = getCommonAncestor (head.left ,O1 ,O2 ); let rightInfo = getCommonAncestor (head.left ,O1 ,O2 ); if (leftInfo !== null && rightInfo !== null ){ return head; } return leftInfo !== null ? left : right; }
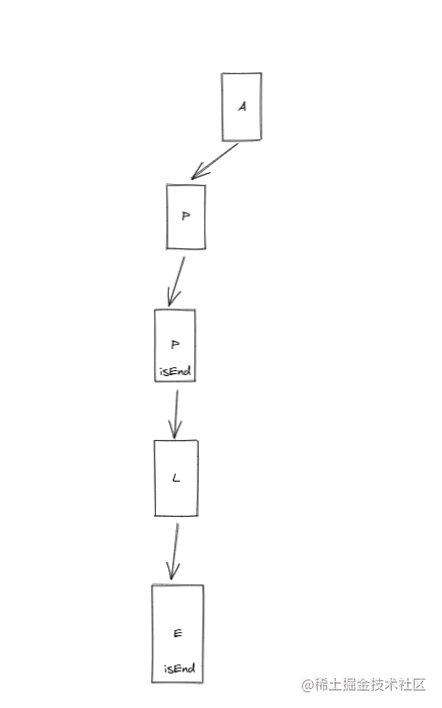
前缀树 例子:
一个arr1:string[],另一个arr2:string[]。arr2中有哪些字符是arr1中出现的?并打印。arr2中有哪些字符是作为arr1中某个字符串前缀出现的请打印,arr2中有哪些字符是作为arr1中某个字符串前缀出现的请打印,arr2中出现次数最大的前缀。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 var Trie = function ( this .tree = {}; }; Trie .prototype insert = function (word ) { let tree = this .tree ; for (const w of word){ if (tree[w] == undefined ){ tree[w] = {}; } tree = tree[w]; } tree.isEnd = true ; }; Trie .prototype search = function (word ) { let tree = this .tree ; for (const w of word){ if (tree[w] == undefined ){ return false ; } tree = tree[w]; } return tree.isEnd == true ; }; Trie .prototype startsWith = function (prefix ) { let tree = this .tree ; for (const w of prefix){ if (tree[w] == undefined ){ return false ; } tree = tree[w]; } return true ; }; var obj = new Trie ()obj.insert (word) var param_2 = obj.search (word)var param_3 = obj.startsWith (prefix)
贪心算法 题目1:有一间会议室,同时被n个团队进行预约,已知每个团队的开始与结束时间,求出一天时间(9点到18点)中最大可以安排多少个团队
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 interface Program { start :number , end :number , } function bestArrange (programs:Program[],timePoint:number ){ programs = programs.sort ((a,b )=> a.end - b.end ); let result = 0 ; for (let i = 0 ; i < programs.lenght ; i++){ if (timePoint <= programs[i].start ){ result++; timePoint = programs[i].end ; } } return result; }